이진 탐색이란?
정렬되어 있는 리스트에서 특정한 데이터를 빠르게 탐색할 수 있도록 해주는 탐색 알고리즘이다.
순차 탐색
리스트 안에 있는 특정한 데이터를 찾기 위해 앞에서부터 데이터를 하나씩 확인하는 방법이다.
가장 기본적인 형태의 데이터 탐색 알고리즘이다. 단순히 데이터를 하나씩 확인한다.
리스트에서 특정 데이터의 존재 여부를 검사할 때 별 다른 말이 없다면 기본적으로 순차 탐색을 이용한다.
이진 탐색
정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법이다.
리스트가 정렬되어 있을 때 사용 가능하다.
이진 탐색은 시작점, 끝점, 중간점을 이용하여 탐색 범위를 설정한다.
이진 탐색 동작 예시

이미 정렬된 10개의 데이터 중에서 값이 4인 원소를 찾아보자.
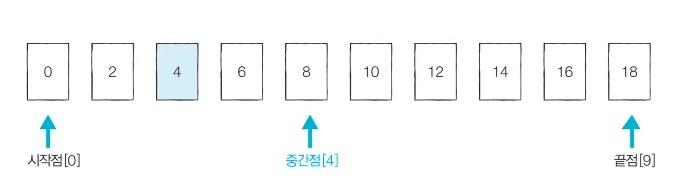
전체 탐색 범위에서 값이 4인 원소를 탐색하는 것이기 때문에 시작점 0, 끝점 9, 중간점 4로 설정한다.
0과 9는 각각의 인덱스를 의미한다. (위치)
중간점이 2개 존재할 수 있는 상황에서는 중간점 인덱스 값에서 소수점 이하는 제거해서 중간점을 설정한다.
중간점 값인 8과 4를 비교해서 어떤 값이 더 큰지 비교한 뒤에
찾고자 하는 값보다 중간점 값이 더 크다면 중간점에서 부터 오른쪽에 있는 값들은 전부 확인할 필요가 없는 것이다.
오른쪽에 있는 값들은 8 이상의 값이기 때문에 찾고자 하는 값인 4보다 더 크기 때문에 중간점의 오른쪽 값들은 볼 필요가 없다.

끝점을 중간점 왼쪽으로 옮긴다.
총 4개의 데이터만 탐색하도록 범위가 좁혀졌다.
이러한 탐색 범위에서 중간점을 찾는다.
현재 중간점은 1이기 때문에 찾고자 하는 값(4)과 비교한다.
중간점 값인 1이 4보다 작기 때문에 왼쪽에 있는 데이터는 볼 필요가 없어진다.

시작점 위치를 중간점 오른쪽으로 옮긴다.
시작점이 2, 끝점이 3이 되어 2개의 데이터를 갖는 탐색 범위가 된다.
중간점 값인 4와 찾고자 하는 값인 4가 동일해지기 때문에 탐색을 마친다.
이진 탐색의 시간 복잡도
단계마다 탐색 범위를 2로 나누는 것과 동일하므로 연산 횟수는

에 비례한다.
한 단계를 거칠 때마다 탐색 범위가 (이상적인 경우) 절반에 가깝게 줄어들기 때문이다.
예를 들어, 초기 데이터 개수가 32개일 때 이상적으로 1단계를 거치면 16개 가량의 데이터만 남는다.
2단계를 거치면 8개의 데이터가 남고, 3단계를 거치면 4개의 데이터만 남는다.
이진 탐색은 탐색 범위를 절반씩 줄이며, 시간 복잡도는 O(logN)을 보장한다.
예시 코드 (재귀함수.ver)
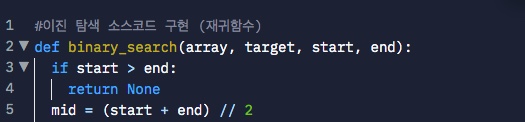
탐색을 수행하고자 하는 배열 정보가 들어오고(array)
찾고자 하는 데이터(target),
탐색 범위가 주어진다. (start, end)
if start > end:
return Nonestart가 end보다 크다면 탐색하고자 하는 범위에 데이터가 존재하지 않는 것과 동일하다.
그렇기 때문에 데이터가 존재하지 않는다는 None 값을 반환하도록 한다.
mid = (start + end) // 2데이터가 존재한다면 (start < end) 시작점과 끝점을 더한 값에 2를 나누어 중간점을 명시한다.

if arrat[mid] == target:
return mid중간점 위치의 값과 찾고자 하는 값이 같다면 해당 값을 찾은 것으로 볼 수 있기 때문에
중간점 인덱스를 반환할 수 있도록 한다.
elif array[mid] > target:
return binary_search(array, target, mid - 1)중간값보다 찾고자 하는 값이 작은 경우 중간점 위치를 포함해
끝점을 중간점 왼쪽으로 옮겨서(mid - 1) 왼쪽부분에 대해서 다시 탐색할 수 있도록 한다.
이와 같이 재귀함수를 이용하여 왼쪽 부분을 탐색한 결과를 반환할 수 있게 한다.
else:
return binary_search(array, target, mid + 1, end)중간값보다 찾고자 하는 값이 큰 경우에는 오른쪽을 확인하도록 한다.
오른쪽을 확인하기 위해 시작점을 중간점 + 1(mid + 1)로 옮긴다.


None값이 반환된다면 탐색 범위가 다 줄어들었음에도 불구하고 원소를 찾지 못한 것이므로
‘원소가 존재하지 않습니다.’로 출럭한다.
해당 원소가 존재한다면 인덱스 값이 반환되기 때문에
1을 더해서 몇 번째 원소인지 출력한다.
예시 코드 2 (반복문.ver)

반복구문이 수행될 때마다 중간점 위치를 확인해서 찾고자 하는 데이터를 찾는다.
찾지 못했다면 탐색 범위를 좁혀가는 방법을 사용한다.
elif array[mid] > target:
end = mid -1중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 부분을 탐색하기 위해
끝점을 중간점보다 1 작은 값으로 바꿔준다.
else:
start = mid + 1같은 로직으로 중간점 <찾는 값 경우 오른쪽 부분을 탐색하기 위해
시작점의 값을 중간점에 1을 더한 값으로 바꿔준다.
파이썬 이진 탐색 라이브러리
- bisect_left(a, x): 정렬된 순서를 유지하면서 배열 a에 X를 삽입할 가장 왼쪽 인덱스를 반환한다.
- bisect_right(a, x): 정렬된 순서를 유지하면서 배열 a에 X를 삽입할 가장 오른쪽 인덱스를 반환한다.

bisect_left를 이용해서 4 원소에 대해 이진탐색을 한다.
4라는 원소가 들어갈 첫 번째 위치인 인덱스 2가 반환되고,
bisect_right을 이용해서 호출하게 되면 원소 4가 들어갈 수 있는 가장 오른쪽 인덱스인 인덱스 4가 반환된다.

값이 특정 범위에 속하는 데이터 개수 구하기

right_index = bisect_right(a, right_value)bisect_right으로 구한 오른쪽 인덱스와
left_index = bisect_left(a, left_value)bisect_left로 구한 왼쪽 인덱스값을
return right_index - left_index빼주게 되면 해당 값에 포함되어 있는 데이터의 개수를 구할 수 있다.
현재 리스트에 포함되어 있는 값들 중에서 left_value와 right_value 사이에 있는 값들의 개수가 반환된다.
print(count_by_range(a, 4, 4))값이 4인 데이터를 출력하고자 한다면 left_value와 right_value을 4로 설정하여
정렬되어 있는 리스트 중에서 4인 데이터의 개수를 출력한다.
파라메트릭 서치 (Parametric Search)
파라메트릭 서치란 최적화 문제를 결정 문제(예 혹은 아니오)로 바꾸어 해결하는 기법이다.
(최적화 문제란 어떤 함수의 값을 가능한 최대한으로 낮추거나 높이는 문제이다.)
문제를 바로 해결하기 어려운 경우 여러번의 결정 문제를 이용해서 문제 형태를 바꾼다.
예를 들어, 특정한 조건을 만족하는 가장 알맞은 값을 빠르게 찾는 최적화 문제가 있다.
현재 범위에서 특정한 조건을 만족하는지 확인하며 탐색 범위를 좁혀가면서 알맞는 값을 찾는다.
일반적으로 코딩 테스트에서 파라메트릭 서치 문제를 이진 탐색을 이용하여 해결할 수 있다.
'이코테 강의 정리' 카테고리의 다른 글
| (이코테 w/ Python) 이진 탐색 문제 풀이 (떡볶이 떡 만들기) (0) | 2022.07.04 |
|---|---|
| (이코테 w/ Python) 정렬 알고리즘 문제 풀이 (0) | 2022.07.02 |
| (이코테 w/ Python) 계수 정렬 (0) | 2022.07.01 |
| (이코테 w/ Python) 퀵 정렬 (1) | 2022.06.30 |
| (이코테 w/ Python) 정렬 알고리즘 - 선택 정렬 & 삽입 정렬 (0) | 2022.06.30 |