떡볶이 떡 만들기 문제 풀이


문제 해결 아이디어
적절한 높이를 찾을 때까지 이진 탐색을 수행하여 높이 H를 반복해서 조정하면 된다.
‘현재 이 높이로 자르면 조건을 만족할 수 있는가? (최소한 M만큼의 떡을 얻을 수 있는가?)'를 확인한 뒤에 조건의 만족 여부(예 혹은 아니오)에 따라서 탐색 범위를 좁혀서 해결할 수 있다.
M만큼의 떡을 얻을 수 없다면 높이값을 더 낮춰서 더 많은 양의 떡이 잘려나가도록 만들 수 있다.
매 높이마다 조건의 만족 여부를 확인해서 조건에 따라서 탐색 범위를 좁히는 방법으로 이진 탐색을 수행하여 최적의 해를 구할 수 있다.
절단기의 높이는 0부터 10억까지의 정수 중 하나이다.
이렇게 큰 탐색 범위를 보면 가장 먼저 이진 탐색을 떠올려야 한다.
(선형 탐색으로 시간 초과 판정을 받을 수 있다)
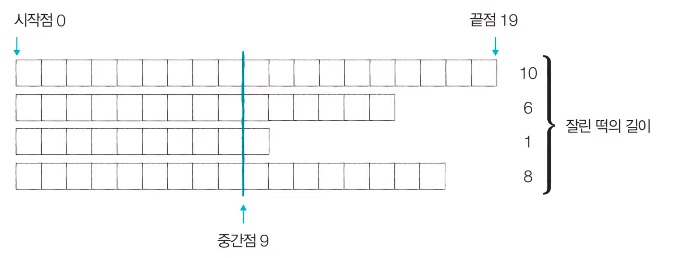
시작점: 0, 끝점: 19, 중간점: 9
필요한 떡의 크기: M = 6
가장 긴 떡의 길이가 19이기 때문에 끝점을 19로 설정한다.
탐색 범위는 0부터 19까지이며
중간점은 자르고자 하는 높이 그 자체가 된다.
중간점(높이)을 9로 설정해서 떡을 자르게 되면 각각의 떡에 대해서 10, 6, 1, 8만큼의 떡을 얻을 수 있다.
이 값들을 모두 더하게 되면 25이기 때문에 필요한 떡이 크기인 6보다 더 큰 값이다.
중간점을 9로 설정했을 때 손님이 요구하는 최소한의 떡이 길이를 맞출 수 있다.
중간점 9를 저장하고 중간점을 더 높여서 잘라본 후 조건을 충족하는지 확인해보자.

시작점을 중간점의 오른쪽(10)으로 옮긴다.
잘린 떡의 길이는 총 9가 된다.
손님이 요구하는 떡의 길이인 6보다 크므로 높이를 14로 설정해서 자랐을 때에도 조건을 만족한다.
(현재의 결과 또한 저장한다)
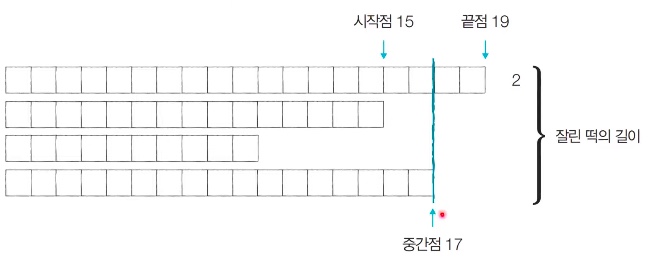
시작점을 중간점의 오른쪽(15)으로 이동한다.
잘린 떡의 값이 2이므로 손님이 원하는 길이인 6을 충족하지 못한다.
그러므로 이 결과값은 저장하지 않는다.

끝점을 중간점의 왼쪽인 16으로 이동한다.
잘린 떡의 길이가 총 6이므로 조건을 만족한다.
현재의 값을 저장하도록 한다.
이와 같이 이진 탐색을 수행하여 더 이상 탐색 범위를 줄이지 못할 때까지 시작점과 끝점의 위치를 바꾸어 가며 높이값(중간점)을 매번 바꾸어보며 조건을 만족할 수 있는지 확인한다.
이진 탐색 과정을 반복하면 답을 도출할 수 있다.
중간점의 값은 시간이 지날수록 ‘최적화된 값'이 되기 때문에 과정을 반복하면서 얻을 수 있는 떡의 길이 합이 필요한 떡의 길이보다 크거나 같을 때마다 중간점의 값을 기록한다.
예시 코드

n과 m의 값의 입력을 받는다.
각 떡의 개별 높이 정보를 입력받는다.

입력으로 들어온 현재 가지고 있는 떡이 높이 중에서 가장 긴 떡의 길이를 end값으로 설정한다.

total = 0
mid = (start + end) // 2
매번 현재 탐색 범위를 이용해서 중간점(높이값)을 설정할 수 있다.
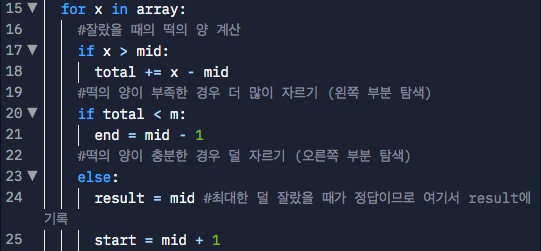
if x > mid:
total += x - mid현재 높이로 떡을 잘랐을 때의 전체 떡의 양을 계산한다.
현재 떡이 길이가 높이보다 더 클 때만 실제로 떡을 얻을 수 있으므로
이러한 경우에만 잘린 떡을 tota 변수에 담는다.
전체 떡을 잘랐을 때 떡의 양 정보가 담길 수 있게 한다.
if total < m:
end = mid - 1떡의 양이 부족한 경우 더 많이 자를 수 있도록 왼쪽 부분을 탐색하도록 한다.
즉, 높이 값이 줄어드는 방향으로 (mid - 1) 탐색 범위를 조절해서 더 많은 양의 떡을 얻을 수 있도록 업데이트한다
else:
result = mid
start = mid + 1얻을 수 있는 떡의 양이 M 이상인 경우 높이값을 더 높여서 덜 자를 수 있도록 한다.
즉, 오른쪽 부분을 탐색하여 높이 값을 키운다.
시작점의 값을 높이+1로 바꿔서 탐색 범위를 바꾼다.
떡의 양이 충분한 경우, m 이상의 떡을 얻을 수 있는 경우 result의 값을 높이값으로 갱신할 수 있도록 한다.

최종적으로 마지막에 기록되어 있는 높이값을 출력하도록 만들면 정답 판정을 받을 수 있다.
'이코테 강의 정리' 카테고리의 다른 글
| (이코테 w/ Python) 이진 탐색 (Binary Search) (0) | 2022.07.03 |
|---|---|
| (이코테 w/ Python) 정렬 알고리즘 문제 풀이 (0) | 2022.07.02 |
| (이코테 w/ Python) 계수 정렬 (0) | 2022.07.01 |
| (이코테 w/ Python) 퀵 정렬 (1) | 2022.06.30 |
| (이코테 w/ Python) 정렬 알고리즘 - 선택 정렬 & 삽입 정렬 (0) | 2022.06.30 |